

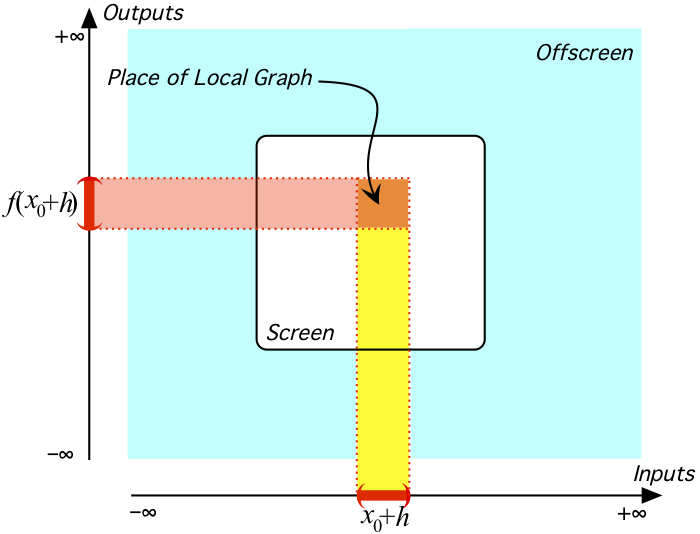
 .
.
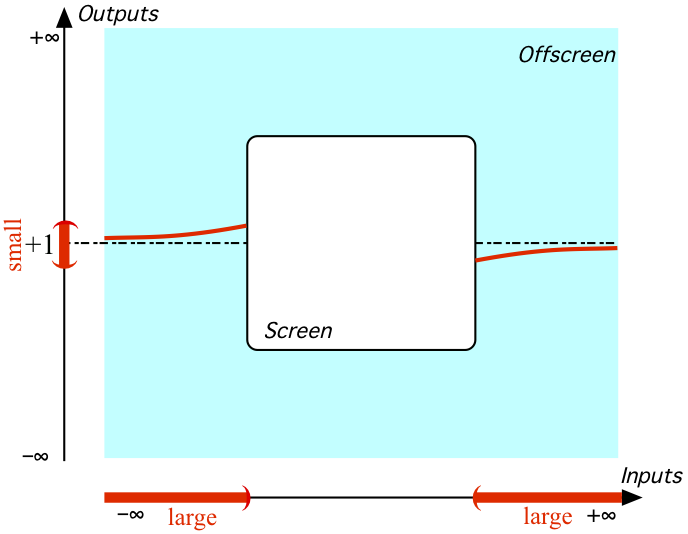
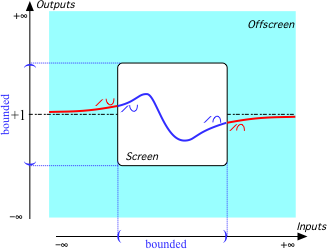
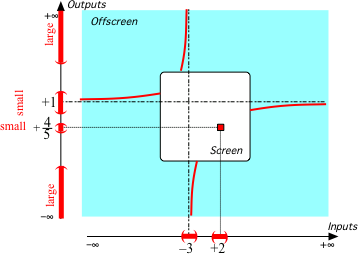
Course content is taken [by many] as given, so the research problem is how to teach it most effectively. This approach [...] has produced valuable insights and useful results. However, it ignores the possibility of improving pedagogy by reconstructing course content. (Emphasis added.)But, as Kipling would have said, that is another story---which I will try to tell in subsequent pieces.