FreeMathTexts.org
For people who want to learn or teach mathematics on the basis of reason …
Chapter Thirteen.
Reasonable Mathematics: A Political Necessity
The following text, which was written under a GNU Free Documentation License, grew out of a short email exchange with B. Atweh. The author is also grateful to the anonymous reviewer of the initial submission who pointed out that "[i]t seems that the author only takes on the issue of quality and assumes that equity comes as a result of [quality]" "Chapter Thirteen" is an attempt at supporting this "assumption".
The tale of how it actually got to be written is told in An Adventure In Academia, in the Notes From The Mathematical Underground and here is the pdf version of the paper which, needless to say, was instantly rejected on the ground that
[I]t is not in a style or content that we are interested in in this publication. [...] [I]t does not have sufficient material on issues of quality and equity.[...] [It is not written in] the standard academic style.
Added on September 19, 2011: The book just came out:
Mapping Equity and Quality in Mathematics Education
by Bill Atweh - Mellony Graven - Walter Secada - Paola Valero, Editors.
--- Springer.
I then emailed the following to Atweh:
"Congratulations on a job well done.
But I hope you will forgive me for remaining skeptical as to how this is going to affect students in the real world, e.g. the world of Pearson."
To which, his response was, in part,
[...]
Foucault has a nice quote that I often use. He says, often I know what I
do. Sometimes I know why I do it. But what I don't know is what I do
does! I guess, this is more true in education than any other vocation.
[...]
Lets all work together towards achieving quality and equity in education
around the globe. I think this is worthwhile.
Well, yes, but ...
13.0 Introduction
Mathematics education has been confronting the problem of how to bring
“quality” mathematics to “the great unwashed masses” for at least thirty years
without any success or even discernible progress. In fact, the only conspicuous
thing is that mathematics textbooks during that time have devolved to
exposition by way of “template examples” and that the subject matter has been
atomized into “independent topics” to facilitate memorization while, typically,
instructors deplore that their students cannot remember the simplest things past
the test.
And yet, it is not difficult to see how just the stress generated by
memorization on the scale required by, say, a year of mathematics must
necessarily have that result: Sisyphus-like, students feel they are starting anew
again and again, topic after topic, and realize there is nothing they can do that
will help them cope with the next topic. Which, of course is why they constantly
ask “Is this going to be on the test?” or complain “You haven’t shown us how to
do that!”.
Nevertheless, the operating, if tacit, assumption is that the great majority of students are incapable of learning on any other basis, least of all on the basis of
intelligence. And by an unfortunate, even if perhaps unavoidable, coincidence,
not only has research in mathematical learning also mostly dealt with isolated
topics but, even more unfortunately, it too essentially equates learning with
memorizing.
In this chapter, we will argue that the alternative “[q]uality mathematics [...]
seen as a reflection of its rigor, formality and generalisability” versus “utilitarian
importance” would seem to be rather beside the point given that there does exist
a third approach in which: i) mathematical quality is ensured by the very fact
that learning is done on the sole basis of a continuous appeal to “reason”,
ii) utilitarian needs are much better addressed in that learning is done by
constant references to the real world and in that a logical mind is very much an
asset in coping with ever-changing practical situations while obsolescence is
built-in into “training”.
However, as the above-mentioned reviewer pointed out, what certainly has to
be shown is how this approach can indeed work for “the great unwashed
masses”.
We will begin by discussing at some length the background against which the
proposed approach was designed and some of the issues that had to be, and were,
taken in consideration. After that, we will present an example of how essential a
role the manner in which the contents are conceived mathematically plays in the
construction of any contents architecture lending itself to the only kind of
“natural” educational enterprise likely to ensure equity. We will then
discuss some of the parameters governing any implementation of such an
approach and briefly present what there already is by way of—freely
available—materials.
13.1 The Only Way Things Can Be?
Quality and equity are usually looked upon as being entirely irreconcilable and
this perhaps nowhere as much as in the U. S. in which the only schools really
open to people of small means, two-year community colleges, do not
even come close to affording the“preparation” necessary to transfer to
schools such as MIT or CalTech or even Harvard, Princeton, Stanford etc.
Considerably worse, there are very large numbers of people whose high
school experience prevents them from entering even two-year community
colleges.
Starting about thirty years ago, an apparent concern for equity
had led to the creation of "developmental"---initially known as
"remedial"programs1.
But the fact is that these programs never even began to work, if by working we
mean affording access to higher education. For instance, at the author’s school, a longitudinal study showed that
the percentage of students entering the development program who eventually
complete Calculus I -Differential Calculus, the “mathematics of change”, is
significantly less than 1%.
In the latter case, one cause is immediately apparent, namely the very length
of the sequence: Starting with, say, Arithmetic, it takes another four semesters,
Basic Algebra (8/9th grade Algebra I), Intermediate Algebra (10/11th grade
Algebra II), College Algebra, College Trigonometry before one can even aspire to
learn Differential Calculus. It also seems that the number of students dropping out of the sequence between courses is comparable to the number of students failing in the courses themselves
A more subtle but in fact much more prevalent cause lies in the already
mentioned deep belief in the necessity to “simplify things” for the students
by atomizing the subject matter into bits and pieces that can then be
“learned” but that can, in fact, only be memorized. And it is precisely this
total reliance on memory that has devastating consequences for equity.
Briefly:
- Forcing the students to rely on memory not only deprives them of the
opportunity to become aware of modus ponendo ponens, that is of the
fact that “if I have this—which I do, then I must also have that” which
is precisely what is necessary for the extension of knowledge, but also of
modus tollendo tollens, that is of the fact that “I cannot have this because
if I did I would then have to have that—which I cannot have” which is
precisely what is necessary for the verification of knowledge.
- Such a massive reliance on memory leads straight to Math Anxiety,
so-called even though it is nothing more than the anxiety of having no
idea of what it is one is forced to do. Not to dwell on the fact that
developmental students generally have little cause to have the trust in
the world and therefore in themselves that is conducive to the peace of
mind necessary for the use of memorized stuff. This necessity of trust alone makes education the privilege of the better off.
Of course, none of which is to say that memory and even “memorization” should not
play any role in whatever “learning” turns out to be, but only that the latter
should not be reduced to the former.
More generally, and whatever the causes, the educational establishment tends
to be extremely elitist in that the prevalent philosophy is that things are the way
they are because, everything else being supposed to have been tried and having
failed, this very absence of alternative “proves” that this is the only way things
can be. Equity is taken to be just a dream. For instance, the inordinate
length of the sequence offered to students in need of arithmetic who
nevertheless wish to learn differential calculus is considered not only
to be an incontrovertible necessity, even if possibly a regrettable one,
but somewhat perversely, also a “proof” that some are mathematically
less gifted than others. Similarly, an even more perverse consequence of
reducing “learning mathematics” to “memorizing disconnected topics”
is very rarely deplored: it is that this disenfranchises the students in
that, rather than leading them to rely on their own common sense, it
habituates them to rely on usually self appointed and hardly disinterested
“experts”.
Closer to the trenches, the lack of success of developmental education is
usually seen as just being the necessary result of the conditions in which
education is taking place. For instance, such things as lack of parental support,
cultural bias, etc are frequently invoked as the root causes for this failure of
memorization even though the connections have never been substantiated and
this merely seems to be the usual teachers’ “moan and groan” at the end of a bad
day.
13.2 Nevertheless, Let’s Be Real!
Aside from all that, there indeed are conditions outside the sphere the profession
can hope to act on and these are all very real and must be acknowledged and
examined, if only for a chance of finding workarounds.
- One the one hand, there are the concrete conditions due to the nature
of our school’s administration, our state’s educational vagaries, the
educational establishment, etc.
One such constraint is that we can have only three, four, possibly, at the very most, five contact hours a week with our students and this for only one or two developmental semesters and there is absolutely nothing we can do about that. Any proposed solution must explicitly fit within this type of schedule.
Another constraint is that this is a one-size-fits-all-students schedule. Yet
any proposed solution must make sure that a sufficient number of students
share enough common reference points most of the time while streaming
essentially eliminates equity. This is actually a most serious issue since it
obviously has a direct bearing on the “success rate” and therefore on the
tolerance our administration, our state and the educational establishment
in general will have for our proposed solution.
And, last but certainly not least, publishers are not about to cease parceling textbooks in order to increase sales by assembling any set of
topics in any order the “better to suit customers needs” where, it ought
to be remembered, the customer is the faculty but it is the student who
foots the bill.
- On the other hand, there are also the constraints due to the nature of the
developmental student population. Privately, most teachers will bemoan
the lack of intellectual capacity of “these people”. They will tell you with
bitter glee the various “you are confusing us”, “you are not teaching us”,
“you are not showing us”, etc awaiting anyone daring to stray in the least
from the “true and tried, show and tell, drill and test” path.
But even if, per chance, these students should somehow deserve more
than memorized indoctrination, even if the shape they are in should only
be the result of twelve years of elementary-secondary education, since
“show and tell” is now “what they want”, this being a free country, “Isn’t
it what we should give them?”
A variant is that these are people most of whom, if not all, have job(s),
families to support, and for whom, in any case, education is not perceived
as really a necessity but, at best, as “what you must get to get a better
job”. And so, “How dare you intrude in their lives?”
So, to use J. Holt’s phrases, the question really is: How do we create a realistic
opportunity (equity) for students to become “question oriented” (quality) in a
framework completely devoted to the production of “answer oriented” students
without infringing on the freedom of the students?
13.3
Meaning, Truth and Consequence
Part of the problem in the U.S. is that it is a country where freedom and individualism are taken to justify one in holding any opinion whatsoever. Other than in court and in graduate school, nowhere is one ever confronted with the need to present one’s case for one’s opinions. In fact, the very idea of truth is
completely eschewed and the very idea of proof completely eliminated. Even the idea of meaning has been held to be ... culture bound, thus subjective, and therefore completely worthless. But, as Colin McGinn has pointed out,
Democratic States are constitutively committed to ensuring and furthering the intellectual health of the citizens who compose them: indeed, they are only possible at all if people reach a certain cognitive level [...] Democracy and education (in the widest sense) are thus as conceptually inseparable as individual rational action and knowledge of the world. [...]. Plainly, [education] involves the transmission of knowledge from teacher to taught. [...]. [Knowledge] is true justified belief that has been arrived at by rational means. [...]. Thus the norms governing political action incorporate or embed norms appropriate to rational belief formation. [...]. The educational system of schools and universities is one central element in this cognitive health service [...].
Thus, once we have decided, for individual or societal reasons, that the main point of mathematics education is that it must provide such a cognitive health service, it becomes completely unthinkable to keep on teaching bits and pieces of mathematics by "show and tell, drill and test" and therefore, by the way, to use the commercially available texts.
So, we must now turn to the two generally accepted---by mathematicians---viewpoints from which to consider and learn mathematics.
- The formalist view, in which mathematics is a game played within a
given set of rules. Z. P. Dienes in Elementary Education and G. Papy in Secondary Education both essentially took that point of view and implemented approaches that were found to be completely accessible to all children inasmuch as playing is nature's way to enforce learning among higher vertebrates including humans. But, aside from the fact that adults don't really like to play, there is also the problem that this framework is completely dependent on the large amounts of time available in primary-secondary educations and would thus seem difficult to adapt to developmental education usually on a very tight schedule.
- The Platonist view, in which mathematics is a sort of rarefied physics in which a paper world is created to mirror the real world and where paper procedures are developed to represent real world processes2.
A priori, this view would appear to be much more adapted to adult education since adults have a much broader knowledge of the real world that can be taken advantage of.
However, by itself, the Platonist view does not ensure that students will learn how to recognize that "this is true" or that "this is false", that "this follows from that" or that :this does not follow from that, etc. After all, physics too can be taught by "show and tell, drill and test".
13.4
The Model-Theoretic View
In fact, as MGinn noted in the article quoted above,
people do not really like the truth; they feel coerced by reason, bullied by fact. In a certain sense, this is not irrational, since a commitment to believe only what is true implies a willingness to detach your beliefs from your desires. [...]. Truth limits your freedom, in a way, because it reduces your belief-options; it is quite capable of forcing your mind to go against its natural inclination. This, I suspect, is the root psychological cause of the relativistic view of truth, for that view gives me license to believe whatever it pleases me to believe. [...]. One of the central aims of education, as a preparation for political democracy, should be to enable people to get on better terms with reason---to learn to live with the truth.
But, initially, one certainly cannot simply appeal to "mathematical proofs" if
only because, as Edward Thorndike showed a century ago, mathematical proofs do not transfer into convincing arguments. Thus, we have what could be called the "McGinn imperative", namely the necessity in the first stage of adevelopmental education in mathematics to reconcile the students with the idea that mathematics is the way it is, not because "experts" say so, but because the real world demands that it be so.
Now, it happens that meaning<, truth, and logical consequence were
defined by Tarski in a classic 1933 paper in which proof becomes the paper
representation of consequence in the real world. Briefly, Model Theory
, which was
born from Tarski's paper, starts with:
- A language, that is a list of nouns and verbs, quantifiers---i.e. for all x, there is at least one x, and connectors---e.g. and, and/or, either one but not both, not---together with syntactic rules for "well-formedness"
- A number of structures, that is, essentially, a number of real world collections of items, each collection coming with a number of relationships and processes. (More about this below.)
Sentences in the language can then be interpreted in any one of these structures and if the sentence describes things as they are in a structure, then the sentence is said to be True under that interpretation and, given two sentences,
S1
and
S2
, we can say that
S1
entails
S2
as consequence if any interpretation that makes
S1
True also makes
S2
True. When dealing with all possible interpretations of the language, we can then speak of logical consequence and
Goedel Completeness Theorem then says that, given a deductive system,
S2
can be proven from
S1
if and only if
S2
is a logical consequence of
S1.
It would thus certainly seem that the model-theoretic view can provide a
framework for a presentation of mathematics for adult learners in that, in such a framework, by constant reference to the real world, adult learners can both:
- make sense of the various issues involved in paper world representations,
- reconcile themselves with the ideas of truth and proof.
And then, as noted by Thurston, students can discover that
Mathematics is amazingly compressible: you may struggle a long time, step by step, to work through some process or idea from several approaches. But once you really understand it and have the mental perspective to seeit as a whole, there is often a tremendous mental compression. You can file it away, recall it quickly and completely when you need it, and use it as just one step in some other mental process. The insight that goes with this compression is one of the real joys of mathematics.
and educators can then discover in turn that compression is the only way that
equity can be reconciled with quality.
Nevertheless, students in developmental programs are enormously insecure
and if a model theoretic view would appear to be necessary to provide a successful road to quality and equity, it is clearly not sufficient and a
"reasonable" version of such a model theoretic approach thus needs to be specified and developed.
Suffice it to say at this point that model theory can be "softened":
- by way of a mode of arguing rather like that used by lawyers in front of
a court. (See S. E. Toulmin's The Uses of Argument.)
- by concentrating on a Coherent View of Mathematics and a Profound Understanding of Fundamental Mathematics. (See L. Ma, Knowing and Teaching Elementary Mathematics: Teachers' Understanding of Fundamental Mathematics in China and the United States )
However, before we can really get to any of that, we must do one last thing and
examine a number of linguistic issues.
13.5 The Language Barrier
In a not too distant past in which there were no printed textbooks, the
transmission of knowledge occurred in the form of a textbook dictated by the
teacher to the students. Per force, the students could thus afford very little
thinking during class and there was no additional communication other than theoccasional Socratic question from the instructor to the students and certainly no
question from the students to the instructor.
Today, things are not really that different and whatever communication there
is usually occurs in the following context: the instructor lectures, the students
take notes, the bell rings, everyone goes home, the instructor to grade
the homework just handed in, the students to do the next homework
from the template examples in the textbook. Clearly, if both quality
and equity are ever to be ensured, another paradigm for communication
is necessary. No longer can the students be simply enjoined to operate
from “template examples” and just told whether the answer is “right” or
“wrong”.
The next issue is that the kind of communication necessary for any attempt
at quality conflicts with equity inasmuch as the natural language of the
developmental student population is completely unadapted to the development of
any mathematical quality however the latter is defined. So, in addition to the
issues already mentioned, mathematical contents and their architecture,
we must now examine a third kind of issues, namely what would have
to be involved in significant, two-way communication on the first two
issues.
- The object language, that is the language used on paper to represent the
real world, must be sufficiently clear to ensure against misunderstandings,
that is not only refer to the aspect of the real world intended by the
sender but also exclude from consideration by the receiver any other
aspect of the real world. This is of course usually done by way of formal
definitions but is not likely to be appropriate with students much given
to “like …you know what I mean”. Thus, just as in all the “trades”, a
specialized language must be developed.
A most important issue here is that the meaning of mathematical
symbols usually depends on the context while students feel of course a lot
more comfortable with context-free terminology, that is with an entirely
one-to-one correspondence between terms and concepts.
An example of a specific issue is that the passage from the active voice,
e.g. Jill beat Jack, to the passive voice, Jack was beaten by Jill, is almost
invariably confused with the more familiar passage to the symmetric
sentence, Jack beat Jill. This is a most important linguistic stumbling
block if only because the passage to the passive voice preserves truth
while the passage to the symmetric sentence need not.
Another linguistic stumbling block is the use of “whose”. For instance,
while Dollar can be defined directly in terms of Quarter by saying “One
Dollar is equal to four Quarters”, the definition of Quarter in terms of
Dollar is an indirect one in that we must say “A Quarter is that kind of
coin of which we need four to change for one Dollar”. The same stumbling
block occurs in dealing with roots since
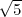 is to be understood as “that
number whose square is 5”.
is to be understood as “that
number whose square is 5”.
Finally, since, as already noted, developmental students are extremely
insecure, once they get started on the road to precision, every single
thing suddenly becomes potentially important to them while they have
not yet reached the point where they can decide what is and what is
not significant and/or what was left unsaid but goes without saying. So,
initially, everything must be completely spelled out including default rules
to deal with what is left unsaid and goes without saying in conventional
mathspeak.
- The meta-language is the language in which we talk about issues of
mathematical contents and issues regarding the way these contents are
related, as seen through paper representations. In contrast with the object
language, the meta-language not only can be a lot closer to the students’
natural language but, in fact, must be so.
But, even there, initially, constant consideration must be given to
the fact that, quite naturally, students cannot be entirely counted on
to realize when they don’t understand something because for them
understanding something means having committed it to memory and,
when asked to explain something, are equally naturally given to taking
refuge in vagueness. Interestingly, though, students almost invariably get
eventually to a point where, with great delight, they nitpick the instructor
to death.
One last aspect of communication in mathematics is that it needs to be
adversarial and this is something difficult to arrive at with students who
initially take it as “disrespect”. Still, the students have to be made to feel
that loose discourse is not only useless but often dangerous.
One difficulty in designing the two languages is in keeping them firmly apart
because, after all, there are only so many words in any natural language and we
need two words for each thing to be named: one for the meta-language and one
for the object-language.
We are now ready to give an idea of how things might work in the classroom.
We begin with the description, as seen in a model theoretic setting, of some mathematical contents and will then offer some comments about how the way mathematical contents are seen mathematically affects the natural learning flow.
13.6 Not So Basic Arithmetic
We start with bunches of items in the real world and pose the problem of how to represent these on paper and how to represent real world processes involving these bunches with paper procedures.
1.
It becomes rapidly obvious that if all the items are of the same kind, in which case we will use the term collection instead of bunch, things become considerably simpler as, in that case, we need only a number-phrase consisting of a denominator to represent the common kind of items and a numerator to indicate the number of items.
For instance, we might represent the collection
 by the number-phrase
by the number-phrase
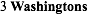
where "3" is the numerator and "Washingtons" is the denominator.
We get the numerator by counting the items in the collection, that is by
reciting a pre-memorized litany, "one, two, three, ..." while touching each one of the items in the collection. Counting is thus a bridge between the real world and the paper world and this is how Arithmetic starts.
By themselves, though, collections and their paper representations are not very interesting and pretty soon we start wondering what kind of things we can do with them.
The first thing one is likely to do is to compare collections which, when the numbers of items are small, is readily achieved in the real world by matching the two collections one to one, that is cardinally. Very soon, though, this turns out to be unbearable and, instead, we start dealing with the number-phrases that represent the collections in the paper world and which we compare by checking the positions of the numerators in the litany, that is ordinally. This is where the standard verbs, <, >, =, ≠, ≦, ≧ are
introduced, characterized in terms of the real world and getting familiarized
with—which they usually very much need to. The negation of sentences
involving these verbs provides the ground for fertile discussions by way of
references to the real world.
The second thing one is likely to do, given an initial collection, is to act on it. For instance, given an initial collection of four dollar bills,

we may want to attach a collection of three dollar bills

and thus get a final collection of seven dollar bills.

Again, soon enough, we move to the paper world and try to specify the paper procedure
for the unary operator that represents attachment and which we call addition-to
4.
For instance, to represent the above attachment, we would use the following addition-to operator:
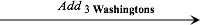
which is, starting in the litany from the input, to count “three” steps, possibly
keeping track on one’s fingers, and then, in order to represent the above attachment, we
would write
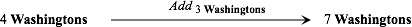
where "4 Washingtons" is the input and "7 Washingtons" is the output.
At this point we can already let the students investigate a number of real world
situations and represent these in the paper world. They can attach a given
collection to various initial collections, they can attach various collections to a
given initial collection, they can chain various addition operators and find to
what single operator an operator followed by another operator is equivalent to,
etc.
The next thing of course is to look at reverse actions namely, here, detachments,
and their paper representations, subtractions from. Immediately, though, we run
into the fact that subtractions from cannot always be carried out which
corresponds to the fact that neither can detachments which says something for
the way the paper world represents the real world.
2.
We then continue with another type of real world situation involving now
two kinds of items from which collections can be made but with a cancellation
effect. For instance, we may look at a banking situation in which we have opening
balances that we can either deposit on or withdraw from and thus get a closing
balances. Naturally, we represent the balances by plain numerators as above but
rather that dealing separately with plain addition and subtraction operators, we
now introduce signed operators. And, if we are rich enough that our bank will
permit us to run deficits, we represent the balances by signed number-phrases
too.
By refering to the real world, developmental students have no difficulty figuring
out, by themselves, the procedures for comparing signed numerators, for
signed addition to and realizing that they all involve as sub-procedures,
the procedures developed earlier in the case of plain numerators: plain
comparison, plain addition to and plain subtraction from. Moreover, it does not
take them long to realize that signed subtraction from is nothing but
signed addition to of the opposite since, when a bank needs to remove a
transaction from a balance, what it actually does is to enter the opposite
transaction:

3. Multiplication is introduced via another kind of real world situation: Given
a collection of items and a unit-price, that is a collection of, say, coins that can be
exchanged for one item, multiplication gives us the total price of the collection at
the unit-price. For instance, we have

This kind of situation can be modified in a natural manner to lead to the “rule of
signs”: Let collections of apples coming into a warehouse be represented on paper
with positive numerators and collections of apples getting out of the warehouse
by negative numerators. Similarly, let the profits to be derived from selling good
apples be represented on paper by positive numerators and the costs to be
incurred by disposing of bad apples by negative numerators. No student
has ever been found who did not agree, instantly, that getting rid of
bad apples was a good thing or, for that matter, who had any trouble
with

4.
The case in which the items are not all of the same kind leads to Linear
Algebra and this is the first occasion in which we reduce a new problem to an
already solved one: The only new idea is that a bunch has first to be decomposed
into collections but, after that, we can represent the bunch by a combination. For
instance, a bunch with two kinds of items, but no cancellation effect, such
as

can be represented in the paper world by the combination
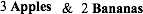
(where & stands in for the more usual but very unfortunate +) or, better yet, by
the basket (aka vector)

After that, essentially, things can be left entirely to the students: Baskets can be
added to and subtracted from in the obvious manner, the passage to
signed-numerators is obvious and multiplication naturally becomes

We would just say that the lists of items as well as the co-lists of unit-prices got
to be of dimension 2 with the total price remaining a scalar and get on our linear
way.
13.6 Comments
The previous section was mostly an attempt at giving the reader some sense of
how a model theoretic view can provide the students with a systematic approach
to things mathematical as opposed to the occasional recourse to “illustrations”
that are invariably and correctly dismissed by the students as ad hoc
gimmicks.
The perceptive reader will of course have already realized not only the many
further implications of what we described in the preceding section but also
noticed the glaring omissions. Given the space limitations, though, we will
discuss only a few of the latter.
1.
At least inititally, many symbols must be used so as to be context-free, which, for instance, is why we use

to distinguish them from
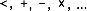
because these symbols each stand for distinct procedures. Somewhere along the line, though, we need to accustom the students to the idea that notations are not hard-wired and that this is in fact fortunate because there is no single notation good for every usage. For instance, at some point, we must fully discuss the identification of positive numerators with plain numerators and appropriate default rules must be explicitly written down. We must also go from
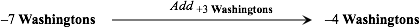
to

and then to just
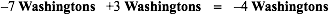
The point, though, is that the longhand will still be there for whenever
something needs to be clarified as well as for when a reference point is needed
later on as, for instance, when functions—in which the underlying procedure
becomes an explicit input-output rule---such as, for instance

are being introduced:
2.
The second glaring omission is that of fractions which actually give us a
further example of the perhaps surprising use of number-phrases. Given that “A
Quarter is that kind of coin four of which we can exchange for one Dollar”, it is
natural to represent a quarter on paper by the denominator
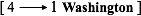
Then, for instance, when the denominators are the same, we have
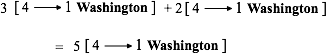
and, if desired,from the built-in definition of a quarter
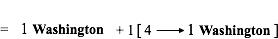
When the denominators are not the same as with, say, three quarters and seven
dimes, to be able to add we naturally need to change the denominators to a common denominator:

Note that with a bit of “preparation” such as exchanging apples and bananas for
strawberries, a notation inspired from co-lists might have made the changes
easier to follow. In any case, at this point, all that remains to do is:
i) to develop
a less ponderous notation, and
ii) to focus on how to get a least common
multiple
3. A third glaring omission is that of the decimal numbers. They are
introduced together with the metric system with money serving as real world
situation. But, aside from the fact that, as engineers are fond to say, “The real
real numbers are the decimal numbers”, the reason decimal numbers are of
the utmost importance to us is that they will be at the core of the local
polynomial approximations which are all we will need to develop a “limit-free”
differential calculus in the manner of Lagrange. See xxx for more on
this.
4. And in fact, for our purposes, fractions are little more than code for
division which bring us to a fourth glaring omission, namely that of the idea of
approximation. Suffice it to say here that we look upon 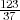 as a shorthand for
“Divide 37 into 123”. This in turns brings the question “What is
as a shorthand for
“Divide 37 into 123”. This in turns brings the question “What is  equal to?”
the response to which is, naturally, “It depends”. For instance, and depending on
the situation, we can write:
equal to?”
the response to which is, naturally, “It depends”. For instance, and depending on
the situation, we can write:
where [...] stands for
something too small to be taken into consideration in the
present situation. It is inspired by, and a first step towards, o
[hn], Landau’s “little
oh”.
13.7 Now What?
We will now conclude with a few practical remarks for anyone intrigued enough
to consider the matter a bit further.
1. A most important thing to keep in mind is that any such
developmental course has zero chance of being successful as a program if
the students are then thrown into “conventional” courses. There is no way
that twelve years of education can be undone in even a whole year. A longer
convalescence is needed. Thus, the reinsertion in a conventional course of
study must occur later and any developmental sequence will require that
further courses be also designed and developed for a smooth transition.
Because of his own mathematical interests and competencies, the particular
course of study that the author chose to implement was that which culminates
with Differential Calculus. An additional reason was that, essentially, the author
had already designed, under a 1988 NSF Calculus Grant, a two semester
sequence as an alternative to the conventional, Precalculus I, Precalculus II and
Calculus I (Differential) sequence. The 1992 report of the author’s school’s Office
of Institutional Research read in part:
Of those attempting the first course in each sequence, 12.5% finished the [conventional three semester 10 hour] sequence while 48.3% finished the [integrated two semester 8-hour] sequence, revealing a definite association between the [integrated two semester 8 hour] sequence and completion (chi square (1) = 82.14, p < .001).
The report also said that the passing rates in Calculus II (Integral) for the
students coming from the above two sequences were almost identical but that
this was not significant because, in both sequences, most students did not
continue into Calculus II (Integral).
What made the two-semester sequence work is directly relevant to the theme of
this chapter in that it was the systematic use of (Laurent) polynomial
approximations (Lagrange’s approach) and that these are of course nothing but
an extension of decimal approximations so that a “profound understanding of
fundamental mathematics”, in this case functions, decimal approximations,
equations and inequations, and (Laurent) polynomials, is all that is necessary
and is likely achievable in one four-hour semester designed along the lines
suggested here.
As a result, a three-semester sequence to replace the six-semester sequence
mentioned at the outset is entirely possible and is in fact what the author is
currently working on.
2. But then, the whole project being a rather radical departure from current
practices, there was Hestenes dictum:
Early in my career, I naively thought that if you give a good idea to competent mathematicians or physicists, they will work out its implications for themselves. I have learned since that most of them need the implications spelled out in utter detail.
So, it was imperative, if anybody was ever to try such an approach, to develop
materials beyond what might have been needed for just a proof of concept. The
author is currently engaged in the production of the materials for the whole
three-semesters sequence.
Some of the materials are available online at http://www.freemathtexts.org.
Having been written in LATEX under a GNU Free Documentation License, they
are therefore freely downloadable, printable, distributable, and modifiable.
However, at this time, they are only standalone forms of parts of the
materials for the three-semester sequence and come in “bundles” currently
formatted for a fifteen week semester meeting twice a week but should not be
difficult to reformat for other schedules. Presumably, they can be used in
Developmental Basic Algebra and Precalculus I - Algebraic Functions
respectively.
A bundle consists of a rather long-winded text divided into eighteen chapters
together with the following “ancillaries”:
- One homework per chapter
- One quiz per chapter
- One Review Discussion for each one of the three parts of the text
- One Review Test for each one of the three parts of the text
- One Exam for each one of the three parts
All the ancillaries are built from a single Question Base of “checkable
items” and keys can be generated. While the ancillaries come out of
the box with lists of checkable items, these lists can be modified and
checkable items added to the Question Base. The format of the ancillaries
can be customized to a significant degree. For instance, the questions
can be presented in random or list order, as open or multiple choice
questions.
3. The author uses these material as follows: The students are to
read a chapter before each class and to do a homework on that chapter.
The class then starts with students questions about the text and the
homework. After about half the time has been thus spent, the instructor hands
out but does not collect a very short quiz, spends some more time on
the chapter and then “introduces” the next chapter. A couple of weeks
before each one of the three exams, the instructor hands out a Review
Discussion with instances of the checkable items to be on the exam,
each being “discussed” at some length. The class before the exam, the
instructor hands out a multiple-choice Review Test consisting of the
exact same questions, although in random order, and checks them on the
spot. The next class is for the exam and, at the end of the semester,
instead of a final, the students can make up any and all exams with the
make up score replacing, for the better or for the worse, the exam score.
Contrary to what one might think, because of the way the questions are
built, this is not a giveaway even though it ought to. But this is another
story.
4. The whole approach is thus heavily predicated on the willingness and the
ability of the students to read the materials. Given that, initially, reading is not
seen by the students as a way to acquire knowledge or even know-how, the first
thing is to get the students used to the idea that they must reach for the text in
order to "understand". But they need help with that and one way is to have the
course linked with a Remedial English Reading course in which the reading
materials is the text in the mathematics course. The link was tried once and the
instructor who had taught the Remedial English Reading course later wrote
that
The students that stayed to the end also appreciated [the approach] whether they passed or not. If we pursue another link, the English teacher should definitely read the math text with the students. Unfortunately, because I had my own reading to do, we did not read the math in English class as we should have done.
5.
At this point, both the developmental course and the PreCalculus course are only
standalone versions of the corresponding materials for a three-semester sequence
ending with Differential Calculus and no statistics exist. Nevertheless, there are
good reasons to think that a three semesters sequence would produce much
better results than the current ones: Given the success-rate mentioned at the
outset, an overall success rate from Arithmetic to Differential Calculus ought, no
matter what, be considerably higher and so it is hoped that people will consider
the approached proposed here.
But then, as Mark Twain [almost] wrote:
When an entirely new and untried educational project is sprung upon the faculty, they are startled, anxious, timid, and for a time they are mute, reserved, non-committal. The great majority of them are not studying the new doctrine and making up their minds about it, they are waiting to see which is going to be the popular side.
(The words he actually used were of course political and people. Not that much of a difference after all.)
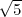 is to be understood as “that
number whose square is 5”.
is to be understood as “that
number whose square is 5”.

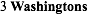



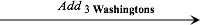
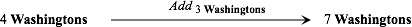




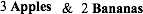



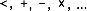
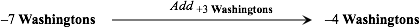

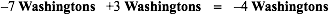

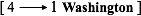
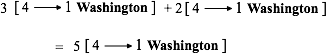
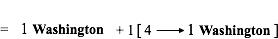

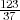 as a shorthand for
“Divide 37 into 123”. This in turns brings the question “What is
as a shorthand for
“Divide 37 into 123”. This in turns brings the question “What is  equal to?”
the response to which is, naturally, “It depends”. For instance, and
equal to?”
the response to which is, naturally, “It depends”. For instance, and